Pythagorean Theorem Trigonometry Proof: Understanding The Relationship Between Geometry And Trigonometry

The Pythagorean Theorem is one of the cornerstones of mathematics, establishing a crucial relationship between the sides of a right triangle. This theorem, attributed to the ancient Greek mathematician Pythagoras, states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. However, the connection between this theorem and trigonometry is equally important, as it lays the groundwork for various trigonometric functions and their applications. Understanding the Pythagorean theorem trigonometry proof not only deepens our comprehension of geometric principles but also enhances our ability to solve complex problems across numerous fields.

Exploring the Pythagorean theorem trigonometry proof opens a window into the fascinating world of mathematics, where geometry and trigonometry intertwine beautifully. By examining the relationships between angles and side lengths, we can apply this theorem to a range of real-world scenarios, from architecture and engineering to physics and astronomy. Moreover, mastering this theorem allows students and professionals alike to develop a strong foundation in mathematics, enabling them to tackle more advanced concepts with confidence.

In this article, we will delve into various aspects of the Pythagorean theorem trigonometry proof. We will explore its historical significance, provide a step-by-step proof, and discuss its relevance in contemporary mathematics. Whether you are a student striving for a deeper understanding of geometry or a professional seeking to refresh your knowledge, this comprehensive guide will illuminate the essential connections between the Pythagorean theorem and trigonometry.

What is the Pythagorean Theorem?

The Pythagorean theorem can be mathematically expressed with the formula: a² + b² = c², where a and b are the lengths of the two legs of a right triangle, and c is the length of the hypotenuse. This theorem is applicable only to right triangles, which contain one angle measuring 90 degrees.

How Did the Pythagorean Theorem Originate?

The origins of the Pythagorean theorem date back to ancient civilizations. Although Pythagoras is credited with its formalization, evidence suggests that the Babylonians and Indians also understood this relationship centuries before him. The theorem has since become a fundamental principle in mathematics, influencing various fields and serving as a basis for further discoveries.

Why is the Pythagorean Theorem Important in Trigonometry?

The Pythagorean theorem is essential in trigonometry because it aids in defining the basic trigonometric ratios: sine, cosine, and tangent. These ratios are derived from the relationships between the angles and sides of right triangles. Understanding the Pythagorean theorem trigonometry proof allows students and practitioners to utilize these ratios effectively in practical applications.

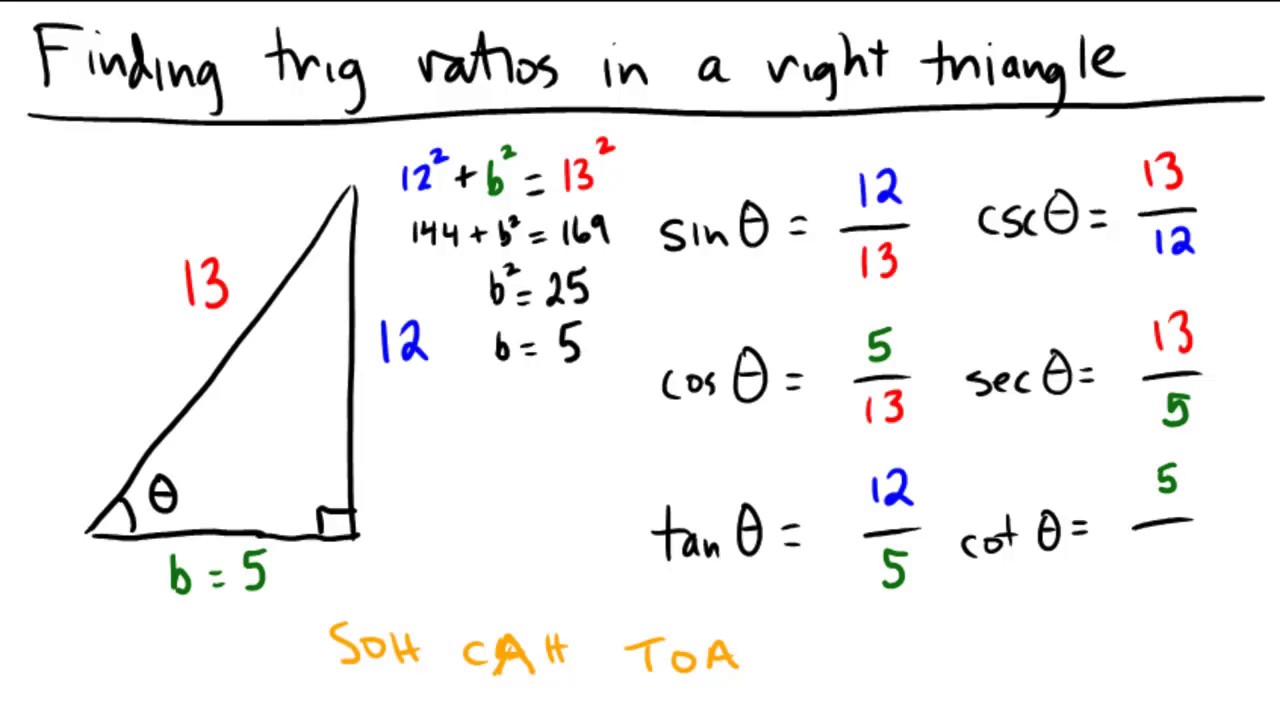
How Can We Prove the Pythagorean Theorem Using Trigonometry?

To prove the Pythagorean theorem using trigonometric principles, we can employ the definitions of sine and cosine. Consider a right triangle with an angle θ, where:

• Adjacent side: the side next to angle θ (length = a)
• Opposite side: the side opposite angle θ (length = b)
• Hypotenuse: the longest side (length = c)

Using the definitions of sine and cosine:

• Cosine of θ: cos(θ) = adjacent/hypotenuse = a/c
• Sine of θ: sin(θ) = opposite/hypotenuse = b/c

From these definitions, we can derive the relationships between the lengths of the sides, leading us to the conclusion that a² + b² = c².

What Are Some Real-World Applications of the Pythagorean Theorem?

The Pythagorean theorem has numerous real-world applications in various fields, including:

1. Architecture: Ensuring structures are built at right angles.
2. Construction: Measuring distances and angles accurately.
3. Navigation: Calculating the shortest paths between points.
4. Physics: Analyzing forces and motion in right-angled triangles.

Can We Explore Other Proofs of the Pythagorean Theorem?

Yes! There are numerous proofs of the Pythagorean theorem, each offering unique insights into its validity. Some popular methods include:

• Geometric Proof: Using rearrangement of shapes.
• Algebraic Proof: Manipulating algebraic expressions.
• Calculus Proof: Using limits and derivatives.

Each proof provides a different perspective on the theorem's fundamental nature, showcasing the richness of mathematical exploration.

Conclusion: Why Understanding the Pythagorean Theorem Trigonometry Proof Matters?

In conclusion, the Pythagorean theorem trigonometry proof is essential in bridging the gap between geometry and trigonometry. By understanding this theorem, we can unlock a deeper comprehension of mathematical principles and their applications in the real world. Whether you're a student, educator, or professional, mastering this theorem will enhance your problem-solving skills and empower you to tackle a wide range of mathematical challenges.

References for Further Learning

If you would like to explore the Pythagorean theorem trigonometry proof further, consider checking these resources:

• Textbooks on Geometry and Trigonometry
• Online courses and tutorials
• Educational videos on platforms like YouTube

By delving deeper into the Pythagorean theorem and its associated proofs, you will not only enhance your mathematical knowledge but also appreciate the beauty and interconnectedness of mathematics as a whole.